神经网络训练的tensorflow实现

本文对神经网络训练步骤等进行说明，并说明了在tensorflow中相应的实现

神经网络训练过程的三个步骤：

定义神经网络的结构和前向传播的输出结果。

定义损失函数以及选择神经网络的优化算法。

生成会话并在训练数据上反复运行神经网络优化算法下面将根据这三部分进行相关概念的解释。

一、定义神经网络的结构以及前向传播结果　

神经网络的结构

主要包括输入输出节点数，以及隐藏层的深度以及每一层的节点数；

前向传播

前向传播就是依据输入以及权重得到输出，前向传播算法如图所示(来自书本)：前向传播算法一般表示为矩阵的形式，输入看成一个１＊２的矩阵$x=[x_1,x_2]$，将$W^{(1)}$表示为一个２＊３的矩阵：

$W^{(1)}= \begin{bmatrix} W_{1,1}^{(1)} & W_{1,2}^{(1)} &W_{1,3}^{(1)}\\ W_{2,1}^{(1)} & W_{2,2}^{(1)} &W_{2,3}^{(1)}\\ \end{bmatrix}$

通过矩阵的乘法，可以得到隐藏层的节点输出为

$a^{(1)}=[a_{11},a_{12},a_{13}]=xW^{1}=[x_1,x_2] \begin{bmatrix} W_{1,1}^{(1)} & W_{1,2}^{(1)} &W_{1,3}^{(1)}\\ W_{2,1}^{(1)} & W_{2,2}^{(1)} &W_{2,3}^{(1)}\\ \end{bmatrix}$

类似的输出层的结果可以表示为：

$[y]=a^{1}W^{2}$

需要注意到是，上面介绍的是线性化的神经网络结构，在应用中有很大局限性，线性模型可以解决的是那些可以用一条直线来划分开的问题,神经网络经常使用使用激活函数实现去线性化.

常用的激活函数

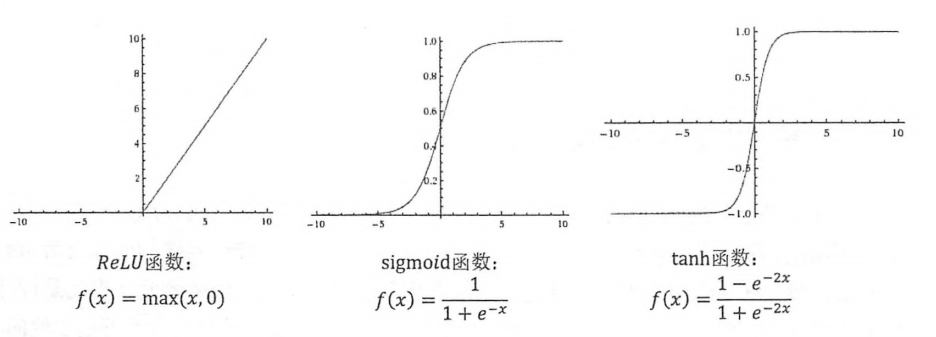与线性模型前向传播的区别在于，每个节点的输出不再是简单的加权和，而是在加权之后经过一个非线性变换，此变换就是所使用的激活函数；同时多了一个偏置项，偏置项的作用是提高网络的鲁棒性（如在分类问题中，有偏置项的时候分类线就不一定过原点，否则必过原点）

tensorflow中相关参数的定义

例如这条代码weights = tf.Variable(tf.random_normal([2,3], stddev))生成一个2×3的矩阵变量，矩阵中的元素是均值为０，标准差为２的随机数。总之在声明变量的时候要给出初始化这个变量的方法．有关参数更多信息，请参考(by 金色暗影)

二、损失函数及反向传播算法

神经网络的训练过程就是参数的设置过程，使用监督学习的方式进行训练．监督学习就是在标注数据集上，模型给出的预测结果要尽可能的接近真是答案．

损失函数

损失函数是用来定义神经网络模型的效果以及优化目标的．对于分类问题，损失函数常定义为交叉熵;　对于预测问题，常用均方误差函数．

交叉熵

交叉熵用来判断输出向量和期望向量的接近程度．给定两个概率p, q．通过q来表示p的交叉熵为：

$H(p,q)=-\sum_{x}p(x)logq(x)$

注意到交叉熵刻画的是两个概率之间的距离，所以我们应该把神经网络的输出转变为概率的形式．可以使用softmax回归实现．softmax回归处理后的输出为：

$softmax(y)_i=y_i^{'}=\frac{e^{yi}}{\sum_{j=1}^{n}e^{yi}}$

通过softmax，神经网络的输出被被用做置信度生成新的输出，新的输出满足概率的所有要求． tensorflow中，交叉熵一般会与softmax一块使用，可以直接通过

cross_entropy = tf.nn.softmax_cross_entropy_with_logits(y, y_)

来计算交叉熵损失函数．其中y表示神经网络的输出，y_表示真实的结果．

均方误差（MSE, mean squared error)

定义如下：

$MSE(y,y^{'})=\frac{\sum_{i=1}^{n}(y_i-y_i^{'})^2}{n}$

其中$y_i$为一个batch中第i个数据的正确答案，$y_i^{‘}$是神经网络给出的预测值．tensorflow中实现均方误差的函数：

mse = tf.reduce_mean(tf.square(y_ - y))

自定义损失函数

tensorflow中支持用户自定义损失函数．更多参考：ensorFlow自定义损失函数(by 修炼之路)

优化算法

优化算法的功能，是通过改善训练方式，来最小化(或最大化)损失函数$E(x)$.

在神经网络的优化算法中，最常用的就是反向传播算法,其流程图如下．

反向传播算法就是一个迭代的过程，每次开始迭代时候，首先取一部分数据作为训练数据，称为batch．batch中的数据通过前向传播得到输出，与真实值对比得到误差，然后根据误差函数进行参数的更新．参数更新算法常选择梯度下降法，通过计算误差函数E相对于权重参数W的梯度，在损失函数梯度的相反方向上更新权重参数．下图展示了梯度下降的原理及过程：根据梯度下降法，参数的更新公式为：

$\theta_{n+1}=\theta_n-\eta\frac{\partial}{\partial\theta_n}J(\theta_n)$

其中，$\theta$是神经网络中的参数，$J(\theta)$是损失函数，$\eta$是学习率，也就是每次参数移动的幅值．梯度下降法可能局部最小，只有损失函数是凸函数的时候才能达到全局最优解，而且计算时间长．随机梯度下降速度快，但是可能找不到最优解，在实际使用的时候经常使用二者的结合，即每次计算一小部分训练数据（batch）的损失函数，tensorflow中的实现函数为：

train_step = tf.train.AdamOptimizer(0.001).minimize(loss)

神经网络的进一步优化

指数衰减学习率

通过指数衰减学习率可以让模型在训练前期快速的接近较优解，又可以保证模型在训练后期不会有太大的波动．tensorflow提供了一种指数衰减法学习率设置方法，其实现函数为：tf.train.exponential_decay,该函数的功能与以下代码功能相同：

decayed_learning_rate = learning_rate*decay_rate^(global_step / decay_steps)

decayed_learning_rate　为每一轮优化时候选择的学习率， learning_rate　是初始学习率；decay_rate是衰减系数，decay_steps　表示衰减速度．函数tf.train.exponential_decay可以通过设置参数staricase选择不同的衰减方式，当staricase被设置为True时，(global_step / decay_steps)会被转化为整数．学习率与迭代轮数的关系如下图：下面给出tf.train.exponential_decay使用的一个示范： learning_rate = tf.train.exponential_decay(0.1, global_step, 100, 0.96, staircase = True) 设置了一个初始学习率为0.1，　每训练100次学习率乘0.96的指数衰减学习率．

正则化解决过拟合问题

神经网络训练的三种情况如图：为了解决过拟合问题，常常使用正则化．正则化的思想是在损失函数中加入刻画模型复杂程度的指标．基本思想是通过限制权重大小，使得模型不能拟合训练数据中的随机噪声．例如在优化的时候常常优化：$J(\theta)+\lambda R(w)$,　其中$R(w)$刻画模型的复杂程度，$\lambda$表示模型复杂损失在总损失中的比例．常用的$R(w)$有两种，分别为L1正则化：

$R(w)=\left\|w\right\|_1=\sum_i \left|w_i\right|$

L2正则化：

$R(w)={\left\|w\right\|_２}^2=\sum_i \left|w_i\right|^2$

tensorflow中计算L1, L2 正则化的损失函数类似，给出L2正则化函数

L2 = tf.contrib.layers.l2_regularizer(lambda)(w)

滑动平均模型

在采用随机梯度下降法训练神经网络时候，使用滑动平均模型可以在一定程度上提高最终模型在测试数据上的表现．tensorflow通过tf.train.ExponentialMovingAverage来实现滑动平均模型．在初始化滑动平均模型的时候，需要设置一个衰减率(decay)，其值越大模型越趋于稳定，实际应用中常常设置为接近为１的数. 为了使模型在训练前期可以更新的更快，ExponentialMovingAverage提供了num_updates参数来动态的设置decay的大小，每次使用的衰减率为：

$\left\{decay, \frac{1+num_updates}{10+num_updates} \right\}$

三、生成会话并运行程序

tensorflow是通过会话(session)来执行定义好的运算的．会话的生成的常用方式有两种,二者的区别以及使用方式如下． 方法一

# 创建一个会话
sess = tf.Session()
# 使用这个创建好的会话来得到关心的运算的结果。比如可以调用sess.run(result),
# 来得到张量result的取值
sess.run(...)
# 关闭会话使得本次运行中使用到的资源可以被释放

方法二

import tensorflow as tf
# 创建一个会话，并通过Python中的上下文管理器来管理这个会话。
with tf.Session() as sess:
    # 使用这创建好的会话来计算关心的结果。
    sess.run(...)
# 不需要再调用“Session.close()”函数来关闭会话，
# 当上下文退出时会话关闭和资源释放也自动完成。

一个完整的神经网络训练的例子是MNIST手写数字识别，请查看源码并对照本文进一步理解．

四、trensorflow模型的持久化

持久化就是让训练好的模型保存下来，然后下次可以直接加载模型，这样就不必每次训练。tensorflow提供了一个很简单的ＡＰＩ来实现这个功能.

持久化代码

通过tf.train.Saver来实现，具体使用方法参考如下代码：

import tensorflow as tf

v = tf.Variable(2,dtype=tf.float32,name="v")
v2 = tf.Variable(2,dtype=tf.float32,name="v2")

for var in tf.all_variables():
    print (var.name)
ema = tf.train.ExponentialMovingAverage(0.99)
maintain_average_op = ema.apply(tf.all_variables())
for var in tf.all_variables():
    print (var.name)
saver = tf.train.Saver()
with tf.Session() as sess:
    tf.global_variables_initializer().run()
    sess.run(tf.assign(v,10))
    sess.run(maintain_average_op)
    saver.save(sess,'model/model.ckpt')
    print (sess.run([v,ema.average(v)]))

保存完之后会出现三个文件，这是因为tensorflow会将计算图的结构和图上的参数分开进行保存。

加载已保存的模型

可以直接加载已经持久化的图以及其参数，实现代码如下：

import tensorflow as tf
#直接加载持久化的图
saver = tf.train.import_meta_graph("/path/to/model/model.ckpt/model.ckpt.meta")
with tf.Session() as sess:
    saver.restore(sess, "/path/to/model/model.ckpt")
    #通过张量的名称来获取张量
    print sess.run(tf.get_default_graph().get_tensor_by_name("add:0"))
    #输出[3.]

当然，持久化的模型可以允许部分加载，以及其他操作，这里不在叙述。需要了解更多操作的话在到网上找。

还是对于ＭＮＩＳＴ手写数字识别问题，这个实现给出了一个最佳的实践样例。将训练与测试分开进行，并使用了一些使代码更易读的方式。

神经网络训练的tensorflow实现