CNN tensorflow

卷积神经网络(CNN)与tensorflow

Posted by cheetaher on May 6, 2019

卷积神经网络

简介

卷积神经网络结构如图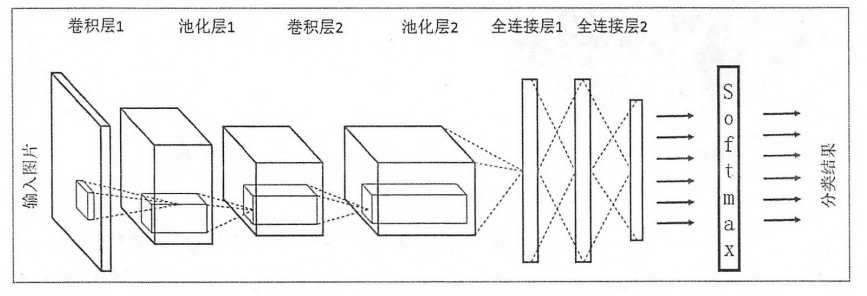： cnn 卷积神经网络与全链接神经网络结构类似，都是逐层前向传递，而且网络的训练过程也十分类似．一个卷积神经网络由５种结构组成，输入层，卷积层，池化层，全链接层，softmax层．

输入层

输入层就是整个神经网络的输入．

卷积层

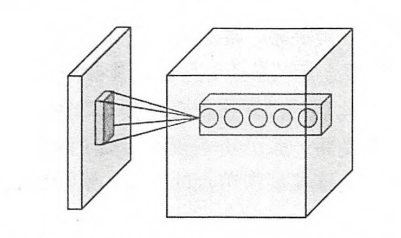
卷积层(concolutional layer)在卷积神经网络中被称为过滤器或者是内核．在tensorflow中卷积层就是称之为过滤器(filter)．过滤器可以将当前层神经网络中的一个子节点矩阵转化为下一层神经网络上的一个单位节点矩阵．单位节点矩阵指长和宽都为１，但是深度不限的节点矩阵．卷积层结构示意图： filter

什么是卷积

由于ＣＮＮ多用于处理图像数据，卷积都是离散形式的卷积．对于在整数Z上的函数f,g，卷积定义为：

过滤器的前向传播过程就是通过左侧小矩阵中的节点计算出右侧单位矩阵中节点的过程．假设$w_{x,y,z}^{i}$表示对于输出矩阵中的第i个节点，过滤器输入节点$(x,y,z)$的权重，使用$b^i$表示第i个输出节点对应的偏置项参数，那么单位矩阵中第I个节点的取值$g(i)$：

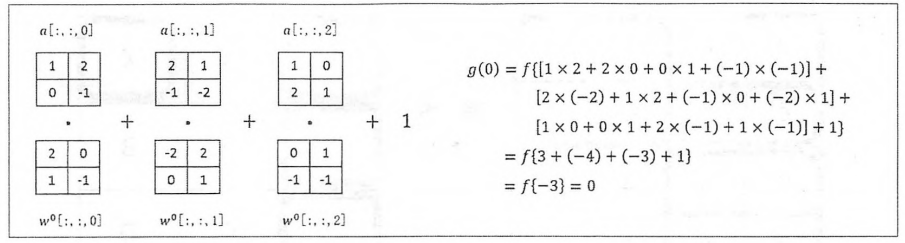其中$a_{x,y,z}$是过滤器中节点$(x,y,z)$的取值，f是激活函数．下图展示了在给定a,$w^0$和$b^0$的情况下，使用ＲｅＬＵ　作为激活函数是g(0)的计算过程．图中的·表示点积，就是矩阵中对应的元素相乘 compute g(0).

卷积层的前向传播

上面介绍了一个过滤器的前向传播，卷积层的前向传播就是通过将一个过滤器从神经网络当前层的左上角移动到右下角，并且在移动的过程中计算每一个对应的单位矩阵得到.下图展示了在33的矩阵上使用22的过滤器时卷积层的前向传播．首先将过滤器用于左上角矩阵，在到右上角矩阵，类似的到右下角，过滤器每次移动一个格子，每移动一次，就可以计算的到一个值（深度为k的时候就会得到k个值）．将这些值拼成一个新的矩阵，就完成了卷积层的前向传播． cnn forwd process

卷积层使用不为１＊１的过滤器时，得到的矩阵会小于当前矩阵，为了让其不缩小，可以使用０补全边缘． 过滤器移动时步长的大小也会影响前向传播得到的矩阵大小，例如长和宽的步长都是２的时候，得到的结果矩阵也只有原来的一半． 注：每一个卷积层使用的过滤器的参数是一样的，这样可以可以巨幅减少神经网络的参数．

tensorflow实现ＣＮＮ　

实现

#通过tf.get_variable的方式创建过滤器的权重以及偏置项．卷积层的参数个数只和过滤器的尺寸，
#深度以及当前层的节点矩阵深度有关,所以这里声明的参数变量是一个四维矩阵，前面两维代表滤波器
#的尺寸，第三个表示当前层的深度，第四表示过滤器的深度
filter_weight = tf.get_variable(
    'weights',[5, 5, 3, 16],
    initializer = tf.truncated_normal_initializer(stddev=0.1))
#和权重类似，偏执层也是共享的，共有下一层深度个不同的偏置项,这里是１６
biases =  tf.get_variable(
    'biases', [16],initializer = tf.comstant_initializer(0.1))
#tf.nn.conv2d实现卷积层的前向传播．第一个输入参数是当前层的节点矩阵; 该矩阵是一个四维的，
#第一个维对应一个输入batch．例如input[0, ;, ;,;,]表示第一张图片，input[１, ;, ;,;,]表示第二张图片,
#后面三个维度对应一个节点矩阵．　　第二个参数提供了卷积层的权重，　　第三个参数为不同维度
#上的步长，该参数是程度为４的数组，注意该数组的第一位和最后一位必须是１．　　　最后一个参数
#是填充的方法．ＳＡＭＥ表示全０填充，ＶＡＬＩＤ表示不填冲
conv = tf.nn.conv2d(
    input, filter_weight, strides = [1, 1, 1, 1], padding = 'SAME')
#给每一个节点都加上偏置项
bias = tf.nn.bias_add(conv, biases)
#通过ＲｅＬＵ去线性化
actived_conv = tf.nn.relu(bias)

池化层

池化层(pooling layer)可以非常有效的缩小矩阵的尺寸，从而减少最后全链接层中的参数．使用池化层既可以加快计算速度也有防止过拟合的作用．

池化层的前向传播

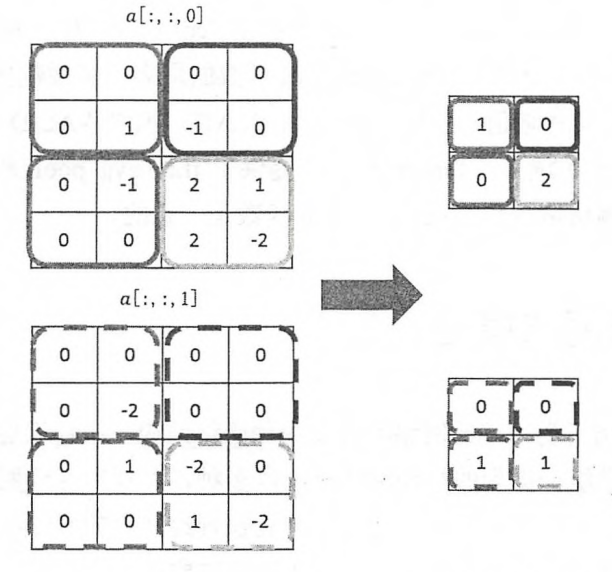
池化层与卷积层类似，也是通过移动一个滤波器来完成的．不同的是过滤器中的计算不是节点的加权求和，而是采用取最大值或者是求平均值．使用最大值操作的池化层被称为最大池化层（max pooling），这种结构使用的比较多．使用平均操作的池化层称为平均池化层(average pooling). 池化层中的过滤器也需要设置过滤器的尺寸，是否使用全０填充以及过滤器移动的步长等，这些设置的意义都是一样的．卷积层和池化层中过滤器的移动是类似的，唯一的区别就是卷积层中的过滤器是横跨整个深度的，而池化层的过滤器只影响一个深度上的节点．所以池化层的过滤器除了在长宽上移动还要在深度上移动．下图展示了最大池化层的前向传播计算过程． pooling forwd process

tensorflow实现
#tf.nn.max_pool实现了最大池化层的前向传播，他的参数和tf.nn.conv2d函数类似
#ksize提供过滤器的尺寸，strides提供步长信息，padding提供是否使用全０填充
pool = tf.nn.max_pool(
    actived_conv, ksize=[1, 3, 3, 1],
    strides=[1, 2, 2, 1], padding = 'SAME')

全连接层

经过几轮卷积与池化之后，可以认为输入图像中的信息已经被抽象成了信息含量更高的特征．可以将卷积与池化看作是图像特征提取的过程，在特征提取完毕后，仍然需要使用全连接层来完成分类任务．

Softmax层

softmax层主要用于分类任务中，可以得到当前样例属于不同种类的概率分布情况． —

经典卷积神经网络模型

LeNet-5模型

LeNet-5模型结构如图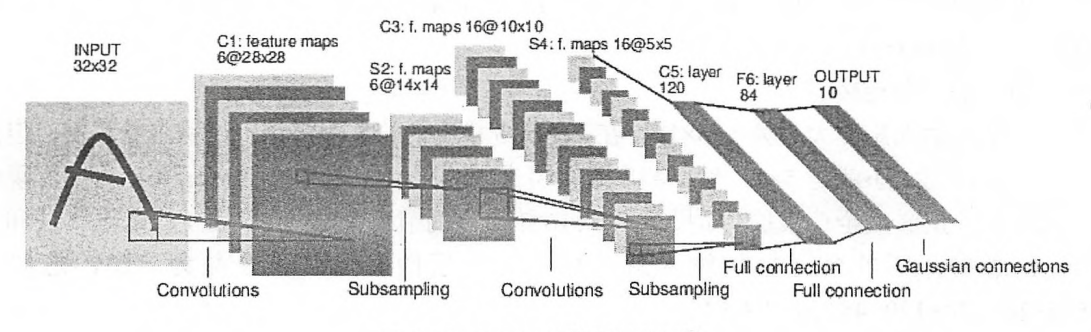： LeNet-5 一共有七层，两层卷积，两层池化，三层全连接层．tensorflow实现的LeNet-5模型． 该模型对手写数字集的识别有很好的效果，但是每一种模型都有其局限性，该模型无法很好的处理较大的图像数据集．

设计卷积神经网络的架构

下面的正则表达式总结了一些经典的用于图像分类问题的卷积神经网络架构： 上面卷积层+表示一层或者多层卷积层，大部分的卷积神经网路中一般最多连续使用三层卷积层，池化层？表示没有或者一层池化层．池化层虽然可以起到减少参数防止过拟合的问题，但是调整卷积的步长也可以实现类似功能，所以有的俊基神经网络没有卷积层．在多层卷积和池化之后，卷积神经网络在输出之前会经过１－２个全连接层．

Inception-v3模型

该模型与LeNet-5模型有较大的区别，在LeNet-5模型中，不同卷积层是通过串联的方式连接在一起，但是在Inception-v3模型中的Inception结构是将不同的卷积层通过并联的方式结合在一起． 我们知道卷积层可以使用边长为１，３或者是５的过滤器，那么如何让在这些边长中选择呢？Inception给出了一个方案，就是同时使用所有不同尺寸的过滤器，然后得到的矩阵拼接起来．下图给出了Inception模块的一个单元结构示意图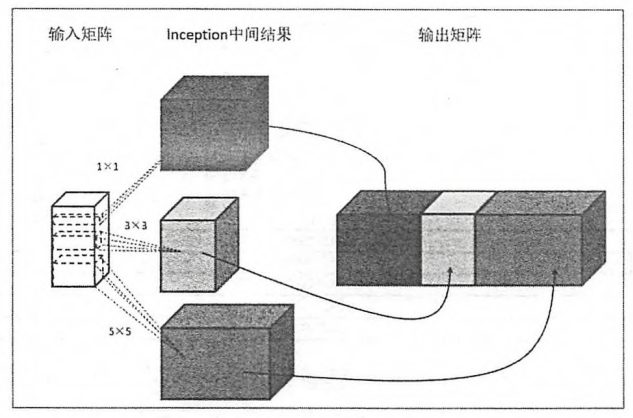． inception 由图可以看出，inception模块首先使用不同尺寸的过滤器处理矩阵，不同的矩阵代表了inception的一条计算路径．虽然过滤器的大小不同，但是若所有的过滤器都使用全０填充，每次移动一步，则前向前向传播得到的结果矩阵的长和宽都合输入矩阵一直，这样经过不同的滤波器处理的结果矩阵可以拼成一个更深的矩阵．Inception-v3模型总共有４６层，由１１个inception模块构成．如下图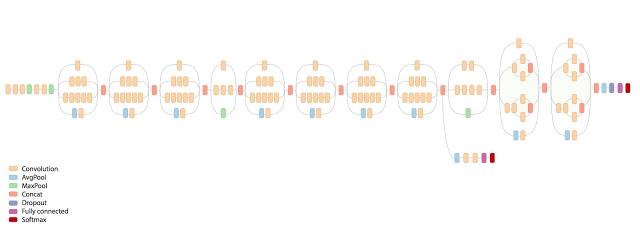： inception-v3 Inception-v3模型的tensorflow实现代码参考．

CATALOG
    FRIENDS